Get a quick overview of Algebraic Identity of (xy)³ and (xy)³ from More Complex Identities in just 3 minutesYou can put this solution on YOUR website!The identity exp(x y) = exp x exp y can fail for Lie algebra elements x and y that do not commute;

Nine To Five Identity Design On Behance
(x y z)^3 identity
(x y z)^3 identity-EduRev Class 9 Question is disucussed on EduRev Study Group by 131 Class 9 StudentsX y is a binomial in which x and y are two terms In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ( x y) 3 = x 3 y 3 3 x 2 y 3 x y 2



Homework 2 With Strategies Homework Eecs 31 Cse 31 Ics 151 Daniel D Gajski S Web Site
F(x, y, z) 132 5y3i (N y — xy)j — (x3yz — xz)k xezi 4yz2j 3yeZk 23 yz In xi (2x — 3yz)j xy z k xyeXi — x3yzezj xy2eYk —x sinyzi z cosxz j ye5XYk In Problems 1—6, graph some representative vectors in the given vector field 3 F(x, y) 6 F(x, y) xi In Problems 17—24, let a be a constant vector and r — xiClick here👆to get an answer to your question ️ Using the identity and proof x^3 y^3 z^3 3xyz = (x y z)(x^2 y^2 z^2 xy yz zx)Use the identity x3y3z3−3xyz=(xyz)(x2y2z2−xy−y z−zx) to determine the value of the sum of three integers given the sum of their squares is 110, the sum of their cubes is 684, the product of the three integers is 210, and the sum of any two products (xyyzzx) is 107 enter your answer as an integer, like this 42
The Baker–Campbell–Hausdorff formula supplies the necessary correction terms Transcendency The function e z is not in C(z) (that is, is not the quotient of two polynomials with complex coefficients) For n distinct complex numbers {a 1, , a n}, the set {e a 1 z, , e a n z} is`64m^3 343n^3` `= (4m – 7n)(4m)^2 4m\xx7n (7n)^2` `= (4m – 7n)(16m^2 28mn 49n^2)` Question 11 – Factorise `27x^3 y^3 z^3 9xyTangent plane to z = 3(x−1)22(y3)27 at (2,−2,12) is given by z−12 = 6(x−2)4(y2) or, equivalently, z = 6x 4y 8 Exc 1443 From ∂z/∂x = 1 2 p y/x and ∂z/∂y = 1 2 p x/y, it follows that ∂z/∂x(1,1) = 1 2, ∂z/∂y(1,1) = 1 2, and hence the tangent plane to z = √ xy at (1,1,1) is given by z −1 = 1 2(x −1) 1 2(y − 1) or, equivalently, x y = 2z 2 Exc 1445
Use the identity x^3y^3z^3−3xyz=(xyz)(x^2y^2z^2−x^y−y^z−z^x) to determine the value of the sum of three integers given Mathematics Answer Comment 1 answer ella 17 5 months ago 5 0 Correctly written, your identity would tell you (sum of cubes) 3·(product) = (sum of integers)·((sum of squares) (sum of any two products)) Filling in the given numbers, you haveIdentity matrix), so that TI(x) = Inx = x for all x 2 Rn Among the more important transformations are those that cause re°ections, projections, and rotations Example 6 Re°ections Consider T R2 7!R2 with standard matrix • ¡1 0 0 1 ‚ then T(x) = • ¡1 0 0 1 ‚ x = • ¡x1 x2 ‚ T re°ects points (x1;x2) about the yaxis What might be the standard matrix of the linear transformati(xyz)^3 (x y z)(x y z)(x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xy y * y = y^2




Algebraic Identities Of Polynomials A Plus Topper




Desidero Identity Redesign By Berkay Dace On Dribbble
(xyz)^3 varify the identity Get the answers you need, now!B) and are associative for all x, y and z in B, x(yz)=(xy)z, and x(yz)=(xy)z c) and are distributive over one another x(yz)=xyxz, and x(yz)=(xy)(xz) d) Identity laws 1x=x1=x and 0x=x0=x for all x in B e) Complementation laws xx'=1 and xx'=0 for all x in B Examples (xyz)^2 using suitable identity 2 See answers devansh00guptaWe know thatx3 y3 z3 3xyz= (x y z)(x2 y2 z2 xy yz zx) Using Identity VIII= (0)(x2 y2 z2 xy yz zx) ∵ x y z = 0= 0⇒ x3 y3 z3If the polynomial k 2 x 3 − kx 2 3kx k is exactly divisible by (x3) then the positive value of k is ____




Note This Book Sample Comprises Of The Cover Page Title Page End User License Agreement Foreword Preface Table Of Contents Editor S Biography And The First Three Pages Of Each Chapter These Sample Images Are In Low Resolution To Optimise The File




Dannewman Xyz Interesting Article By Zhenpixels About The 1987 Apple Identity Guidelines T Co Z5ikf3xkxy
Simplify (xyz)^2 Rewrite as Expand by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply by Multiply by Multiply by Add and Tap for more steps Reorder and Add and Add and Tap for more steps Reorder and Add and Add and Tap for more steps Reorder and Add and Move MoveUse the identity x^3y^3z^3−3xyz=(xyz)(x^2y^2z^ 2−xy−yz−zx) to determine the value of the sum of three integers given the sum of their squares is 110,the sum of their cubes is 684, the product of the three integers is 210,and the sum of any two products (xyyzzx) is 107 Answers 1 Get Other questions on the subject Mathematics Mathematics, 1800, xojadeWe know here today that using a tin tripping, electric identity and C equals negative 10 April's 10 be over one minus 10 8 times 10 b There's a trigger electric identity for tangent out wide in the textbook Therefore, we know that we can rewrite this as tan of sea Or, in other words, we can consider that to be Z one minus tan axe 10 Be so so we're using X, y and Z, or you can also use




Ex 9 5 2 Class 8 Find The Product Xyz 4 Xyz 2 Using Algebra




Solved Provide The Missing Reasons Select Division Property Of Equality Identity Substitution Multiplication Property Of Equality Given Given Xyz With Xy Trisected At P And Q And Yz Trisected At R And Axyz
X Y Z 3 Identity, CategoryIF1 Mazes Identity Fraud Wiki Fandom, The SEO Cyborg How to Resonate with Users & Make Sense to, The SEO Cyborg How to Resonate with Users & Make Sense to, xxxxxxxxxxxxx na FikcjaMia#1678 with the little !Transcribed image text POPOLE The identity element is Y Determine the inverse, if it exists of (a) (b) Y, and (c) Z UL х Y Z х Z х Y Y х Y Z Z Y Z X (a) Select the correct choice below and, if necessary, fin in the answer box to complete your choice O A The inverse of Xis OB The inverse of X does not exist (b) Select the correct choice below and, if necessary, na in the answer box




Polynomials Ppt Video Online Download




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5
I don't know exactly what to do to obtain a geometric proof (of course many proofs exist eg using convexity of the exponential function), but to relate the quantities via linear algebra I suggest $$ \det\pmatrix{x & y & z\\ y& z& x\\ z & x & y} =3xyz(x^3y^3z^3)$$Using Identity VIII x 3 y 3 z 33xyz= (xyz)(x 2 y 2 z 2xyyzzx) solve the following question 8x 3 y 3 27z 318xyz;Answer (1 of 5) First of all, we observe the following formula {{\left( a\,\,b \right)}^{\,3}}\,=\,{{a}^{\,3}}\,\,{{b}^{\,3}}\,\,3\,a\,b\,\left( a\,\,b \right




Pinniped Kubernetes Single Sign On With Openid Connect Linuxblog Xyz



Mirror Xyz Review How To Use Metamask To Compete In The Write Race Consensys
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yz👍 Correct answer to the question Prove the identity x^3 y^3 z^3 2xyz = ( xyz) (x^2 y^2 z^2 xy yz xx) eanswersin




Using Identities Prove That X Y Z 2 Is Greater Than Or Equal To 3 Xy Yz Zx Maths 419 Meritnation Com




Simplify X Y Z 2 X Y 2 Z 3 2 X 2 Y 3 Z 4 2
Correct answers 1 question Use the identity x^3y^3z^3−3xyz=(xyz)(x^2y^2z^ 2−xy−yz−zx) to determine the value of the sum of three integers given the sum of their squares is 110,the sum of their cubes is 684, the product of the three integers is 210,and the sum of any two products (xyyzzx) is 107View Full Answer 8x3y327z318xyz = (2x)^3 (y)^3(3z)^3 3 (2x)(y)(3z) = (2xy3z) (4x^2y^29z^22xy3yz6xz) 0 ;Sep 03,21 The identity of x^3 y^3 z^33xyz is (x y z)(x^2 y^2 z^2xyyzzx)?




Solved Assignment 1 1 Construct A Truth Table For The Chegg Com




How To Prove Xyz 1 3 Le X Y Z 3 Using Linear Algebra Mathematics Stack Exchange
Share with your friends Share 1 0 ;Correct answers 1 question Use the identity x^3y^3z^3−3xyz=(xyz)(x^2y^2z^ 2−x^y−y^z−z^x) to determine the value of the sum of three integers given the sum of their squares is 110, the sum of their cubes is 684, the product of the three integers is 210, and the sum of any two products (xyyzzx) is 107 (xy)^3 (yz)3 (zx)^3 = 3(xy)(yz)(zx) That is it no constraints etc It mentions "This can be done by expanding out the brackets, but there is a more elegant solution" Homework Equations The Attempt at a Solution First of all this only seems to hold in special cases as I have substituted random values for x,y and z and they do not agree




Simple Semirings




Algebraic Identities Of Polynomials A Plus Topper
X(y z) = xy xz multiplicative identity x (x) 1= x multiplicative property of zero x (x) 0= 0 additive identity x 0= x multiplicative inverse x (x) 1/x = 1 additive inverse x (x) = 0 definition of subtraction xy = x (y) definition of division x/y = x (x) 1/y multiplicative property of 1 x(1) = x additive property of equality 3x 2 = 8 3x 22 = 8 3x = 6This video shows how to evaluate using the identity'x3y3z33xyz=(xyz)(x2y2z2xyyzzx)'To view more Educational content, please visit https//wwwyoutWe know here today that using a tin tripping, electric identity and C equals negative 10 April's 10 be over one minus 10 8 times 10 b There's a trigger electric identity for tangent out wide in the textbook Therefore, we know that we can rewrite this as tan of sea Or, in other words, we can consider that to be Z one minus tan axe 10 Be so so we're using X, y and Z, or you can also use




Inequalities Anthony Erb By Arturo Portnoy Issuu




10 Simple Ways To Develop A Spiritual Practice Or Identity By Ariessign Xyz Zodiac Signs Astrology Signs Zodiac Birth Dates
What must be subtracted from 4x^42x^36x^22x6 so that the result is exactly divisible by 2x^2x1?On x^3 x y^3 y = z^3 z Suppose we wish to find an infinite set of solutions of the equation x^3 x y^3 y = z^3 z (1) where x, y, z are integers greater than 1 If z and x are both odd or both even, we can define integers u and v such that z=uv and x=uv Substituting into equation (1) gives y^3 y = 2v(3u^2 v^2 1) Since v divides the righthand side, it would be nice if it Using identity a 3 b 3 c 3 3abc = (abc)(a 2 b 2 c 2 ab bc ca) (xy) 3 (yz) 3 (zx) 3 3(xy)(yz)(zx) = (xy yz zx) (xy) 2 (yz) 2




Akacieholm Realestate Identity On Behance




Evolvit Brand Identity Guidelines By Nazmul Hossan On Dribbble
Rewrite (x−y −z)2 ( x y z) 2 as (x−y−z)(x−y−z) ( x y z) ( x y z) Expand (x−y−z)(x−y−z) ( x y z) ( x y z) by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply x x by x xLHS = x3 y3 z3 3xyz= (x y x) (x2 y2 z2 xy yz zx) Using Identity VIII (xyz){2x2 2y2 z2 xy yz zx) (xyz){2x2 2y2 2z2 2xy 2yz 2zxAnswerUsing the identity and proof x3 y3 z3 3xyz = (x y z)(x2 y2 z2 xy yz zx) Stepbystep explanationI give you answer now it is your d jailan443 jailan443 Math Secondary School X^3y^3z^33xyz complete the identity 2 See answers




Let G X E R X 1 Be The Set Of All Real Numbers Greater Than 1 For X Y E G Define X Y Xy X Y 2 1 Show That The Operation Is




Pdf Leadership Storytelling Event As A Means Of Prompting Organizational Identity Change Semantic Scholar
Use the identity x3y3z3?3xyz=(xyz)(x2y2z2?xy?yz?zx) to determine the value of the sum of three integers given the sum of their squares is 110, the sum of their cubes is 684, the product of the three integers is 210, and the sum of any two products (xyyzzx) is 107 Enter your answer as an integer, like this 42Using the identity `x^3 y^3 = (x y)(x^2 xy y^2)` We get `27y^3 125z^3` `= (3y 5z)(3y)^2 3y\xx5z (5z)^2` `= (3y 5z)(9y^2 15yz 25z^2)` (ii) `64m^3 343n^3` Answer Given; Factorise 8x^3y^3z^36xyz using identity anala81 is waiting for your help Add your answer and earn points
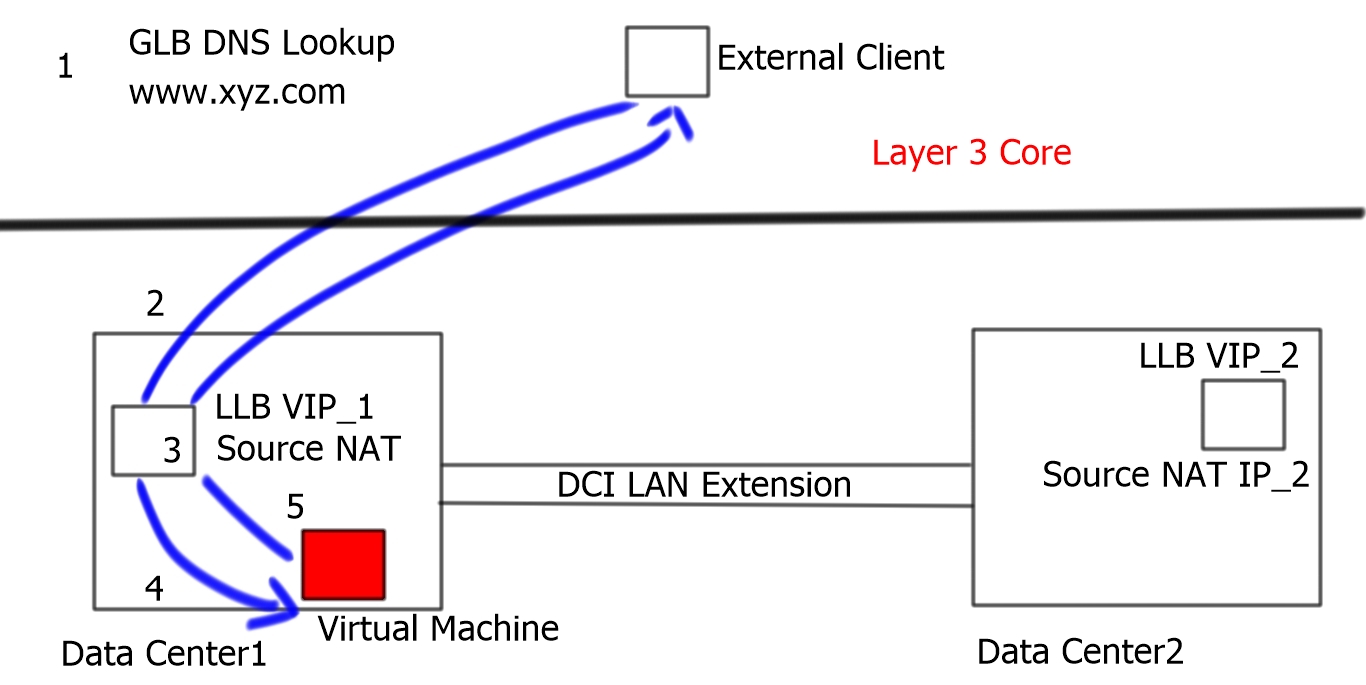



Hairpinning Triangular Routing Locator Identity Separation Protocol Lisp




H C Turk Thedirtgod Thank You Faces With Deep Identity Stare Blankly Through You 1 T Co Cf9uusc9hi 2 T Co 25xasn91qx 3 T Co Axlqa801vn 4 T Co Quod5keyzv Dirtgodfriday T Co Muxe5jktgs Twitter
By AMGM $$ \frac{xyz}{3} \geq \sqrt3{x y z} $$ Now take the cubic value on both sides of this inequality Use the following identity which also gives you the exact deviation in positive terms from $27 x y z$ (from which you can derive tighter bounds of the LHS) $$ (xyz)^3 = 27 x y z 3 Use the identity x^3y^3z^3−3xyz=(xyz)(x^2y^2z^ 2−xy−yz−zx) to determine the value of the sum of three integers given the sum of their squares is 110,the sum of their cubes is 684, the product of the three integers is 210,and the sum of any two products (xyyzzx) is 107 Now we plug in all the values in the identity 684 3(210) = (xyz)() 684 630 = (xyz)(3) 54 = 3(xyz) Divide by 3 on both sides 18 = xyz the value of the sum of three integers is 18 New questions in Mathematics I just need the answers to these and I'll be done with my homeworkPlease help heyy ppl u should add me on discord !



Silent House Productions Logo Visual Identity Brent Lambert




Use The Identity X A X B X 2 A B X Ab To Find The Following Products I X 3 X 7 Ii 4x 5 4x 1 Iii 4x 5 4x 1 Iv 4x 5 4x 1 V 2x 5y 2x 3y Vi 2a 2 9 2a 2 5 Vii Xyz 4 Xyz 2
Ex 25, 13 If x y z = 0, show that x3 y3 z3 = 3xyz We know that x3 y3 z3 3xyz = (x y z) (x2 y2 z2 xy yz zx) Putting x y z = 0, x3 y3 z3 3xyz = (0) (x2 y2 z2 xy yz zx) x3 y3 z3 3xyz = 0 x3 y3 z3 = 3xyz Hence pro




Securing Azure Lighthouse With Azure Policy And Azure Privileged Identity Management For Msp S And Customers Laptrinhx



1 Sjsjsjjsjdjdjsjssj 2 Hi Lol 3 So Are You Love Http Www Quizprank Xyz Message Php Id Fu6l85g0 My Teen Chats




How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube




Z Letter Icon Zeibe Brand Identity By Pexels Pro On Dribbble




Ultimate Brand Creation Corporate Identity Case Study For Brand Identity Design Services Ppt Inspiration Background Images Pdf Powerpoint Templates




Prove That 1 1 1 X Y Z X 3 Y 3 Z 3 X Y Y Z X Y Z




Ex 2 5 Q No 12 Verify X3 Y3 Z3 3xyz 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Solution Briefs Archives Page 3 Of 3 Securonix
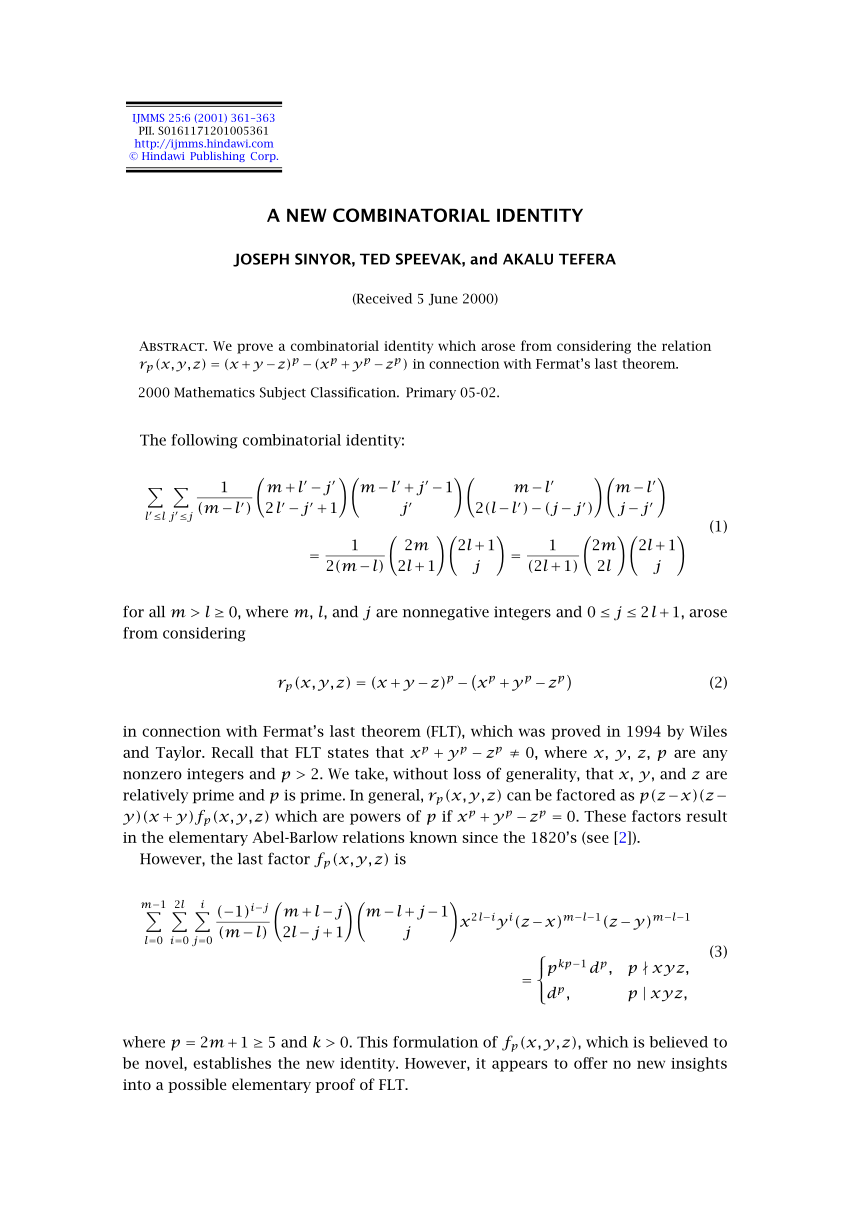



Pdf A New Combinatorial Identity



The Fig 1 Shows Ring Signature User Allocation System When User Logged Download Scientific Diagram




Solved V Boolean Algebra 1 Derive This Identity X X Y Chegg Com



Explaining The Iota Identity Actor




Assignment On Algebraic Identities Pdf
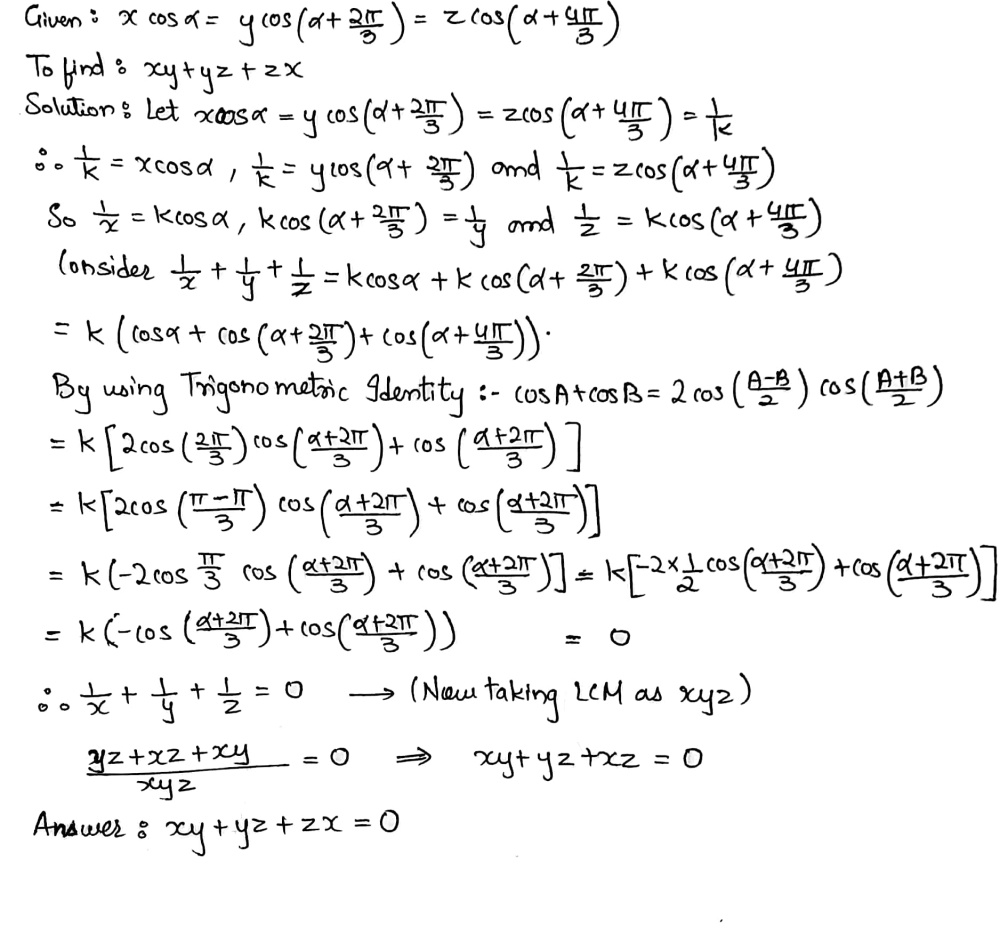



If Scos Alpha Ycos Text 61 Alpha Frac 2pi 3 Zcos Left Alpha Frac 4pi 3right Then Find The Value Of Xy Yz Zx Snapsolve




Solved Q5 Let X Y And 2 Be Subsets Of Universal Set U For This Question Fou Will Prove The Following Set Identity In Two Ways Xuz Y Yux N Yuz 3 Points Use The




Solved Prove The Identity Assuming That The Appropriate Partial Derivatives Exist And Are Continuous If F Is A Scalar Field And Textbf F Textbf G Are Vector Fields Then F Textbf F Textbf F Cdot




Symmetric Polynomial Identities X Y Z N In Terms Of Sigma 1 X Y Z Sigma 2 Xy Yz Xz And Sigma 3 Xyz Mathematics Stack Exchange



You Are A Us And Xyz Citizen Do You Receive Protection From The Us Embassy If You Entered The Xyz Territory With Your American Passport Quora




Maths Identity 8 Polynomial Part 12 English Youtube




Identity Parameter An Overview Sciencedirect Topics




Sensors Free Full Text Identity Based Key Exchange On In Vehicle Networks Can Fd Amp Flexray Html




Use The Divergence Theorem To Find The Outward Flux Of The Vector




Solved Questions 1 Demonstrate By Means Of Truth Tables Chegg Com




Using Identity Viii X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Solve The Following Question 8x3 Y3 27z3 18xyz Maths Polynomials Meritnation Com



2




Optimization Pre Mid Term Flashcards Quizlet




Rento Xyz Brand Identity Domestika




Solved 2 Simplify The Following Functional Expression And Chegg Com
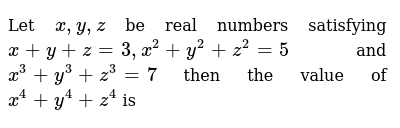



Let X Y Z Be Real Numbers Satisfying X Y Z 3 X 2 Y 2 Z 2 5 And X 3 Y 3 Z 3 7 Then The Value Of X 4 Y 4 Z 4 Is




Personas Frequently Asked Questions Segment Documentation



Brand Equity Model Template Creately



1




Solved 8 3 Prove Algebraically The Following Identity X Yz Chegg Com



Homework 2 With Strategies Homework Eecs 31 Cse 31 Ics 151 Daniel D Gajski S Web Site




If X Y Z 0 Show That X 3 Y 3 Z 3 3xyz With Video




Trigonometric Identities List Of Trigonometric Identities Examples




Nine To Five Identity Design On Behance




Polynomials Ppt Video Online Download



1




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Use The Identity X A X B X 2 A B X Ab To Find The Following Products I X 3 X 7 Ii 4x 5 4x 1 Iii 4x 5 4x 1 Iv 4x 5 4x 1 V 2x 5y 2x 3y Vi 2a 2 9 2a 2 5 Vii Xyz 4 Xyz 2



The Android Style Guide And Google S Emerging Identity Phonearena




Solved Question 4 Let G Be A Group And Xy Z Elements Of G Such That Xyz E The Identity Element Which Of The Following Must Necessarily Also Be Equal To E Choose




Solved Let 2 X 1 Y 1 Z 1 What Is The Value Of Za Chegg Com




If X Y Z 0 Then Find The Value Of X 3 Y 3 Z 3 Maths Algebraic Expressions And Identities Meritnation Com




Tinkutara Equation Editor Math Forum Question 6809




If X Y Z 0 Then Show That X Cube Y Cube Z Cube 3xyz Mathematics Topperlearning Com Vj2f0044
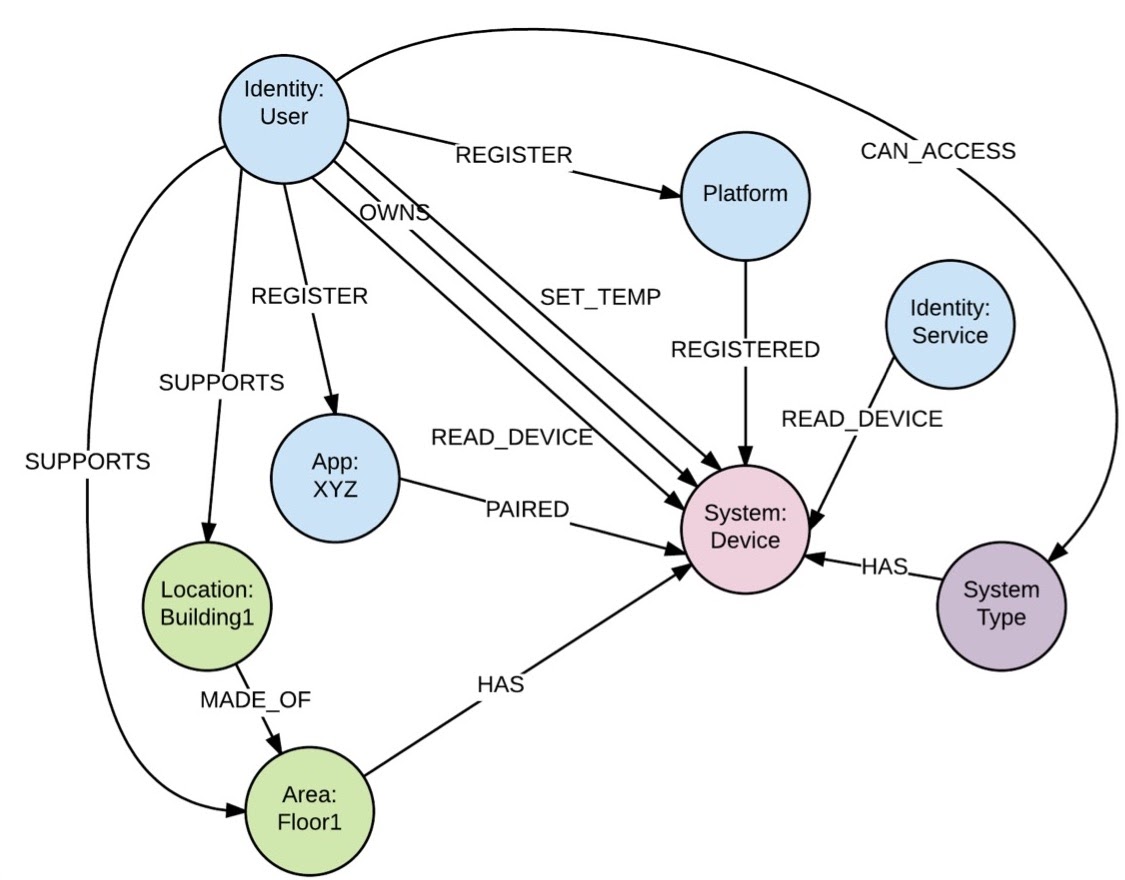



Using Graphql For Digital Identity Access Management




Xyz Storage Identity




Star Icon Starrap Brand Identity By Pexels Pro On Dribbble




A By Quest Journals Issuu



2




Calculus 3 Divergence And Curl 31 Of 50 Identity 7 Curl Curl F Grad Div F Grad 2 F Youtube



Portal Usahockey Com



Ungm Org




Solved Q5 Let X And 2 Be Subsets Of A Universal Set For This Question You Will Prove The Following Set Identity In Two Ways Uy Z Zux N Zuy 3 Points Use The




Csi Technology Group Identity Federation Standards And Justice Information Sharing Csi Technology Group Participates In Highlighted Ijis Project With The Growing Visibility And Importance Of Identity Management Security And Privacy It




Vii X Y Z 4 X Y Z 2 Find The Following Squares By Using The Identities Begin Array L L L L




Introduction To Robotics By Ed Red A Robot




Maite Studio Brand Identity On Behance Typography Inspiration Typography Design Typography Packaging




If X Y Z 0 Show That X3 Y3 Z3 3 Xyz Brainly In




Solved 1 Construct A Truth Table For The Following A Xyz Chegg Com




Project 3 Identity Through Type Hurley Woodford
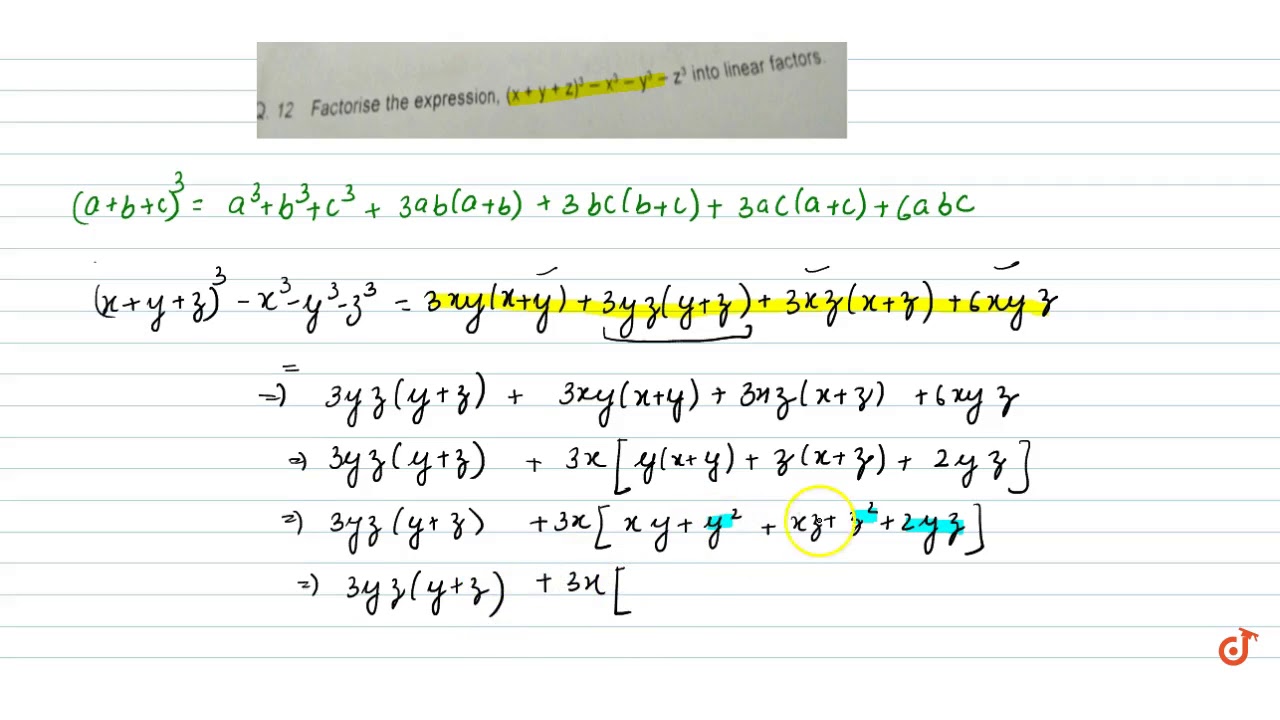



Q 12 Factorise The Expression X Y Z 3 X3 Y3 Z3 Into Linear Factors Youtube



2




Revised Social Media Policy
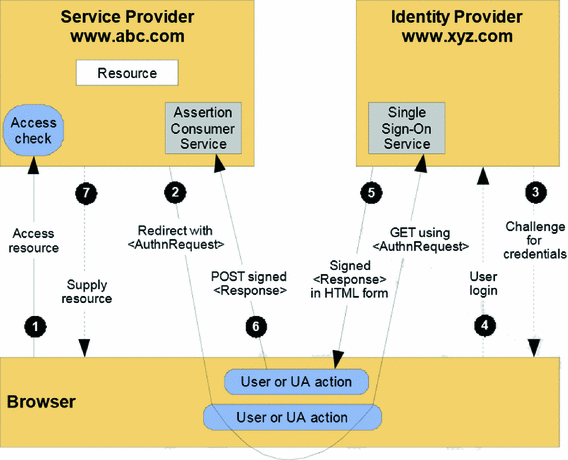



Enhancing Public Digital Identity System Spid To Prevent Information Leakage Springerlink




M Letter Logo Memount Brand Identity By Pexels Pro On Dribbble




3 Ways To Create A Logo Design Xyz Domain Names Join Generation Xyz




Mirror Xyz Review How To Use Metamask To Compete In The Write Race Consensys



Is The Gauss Elimination Method X 2y 3z 1 2x 3y 8z 2 X Y Z 3 Quora



Mirror Xyz Review How To Use Metamask To Compete In The Write Race Consensys




Solved 11 Iii 5a 7 5a 7 1 2m 0 3 1 2m 0 3 Vii 6y 7 6y 7 Iv 3p 2 3p 2 Vi X Y X Y Viii 70




K Electrical Branding On Behance Brand Book Logo Guidelines Corporate Identity Design




18 Algebraic Identities Of Polynomials Ideas Polynomials Identity Solution Examples



0 件のコメント:
コメントを投稿